

Trapping Rain Water Problem
Get started
জয় শ্রী রাম
🕉What is Lower Envelope ?
Given a set of N unsorted, unordered line segments, the lower envelope of these line segments will be the collection of the lowest points (i.e, points with lowest y-coordinates) in the plane.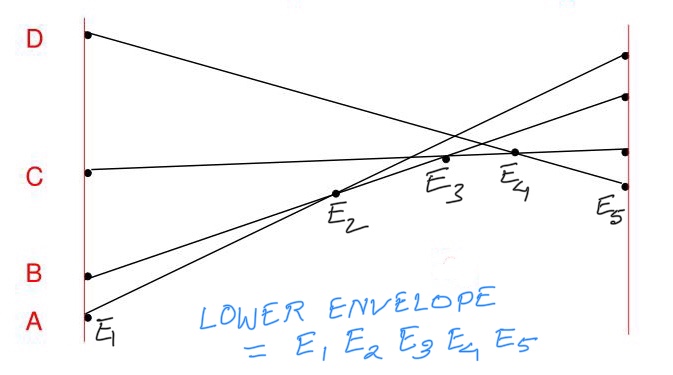
We can easily compute Lower Envelope using Sweep Line Algorithm.
We will discuss a problem below where we will be using Lower Envelope concept to solve the problem.
Problem Statement:
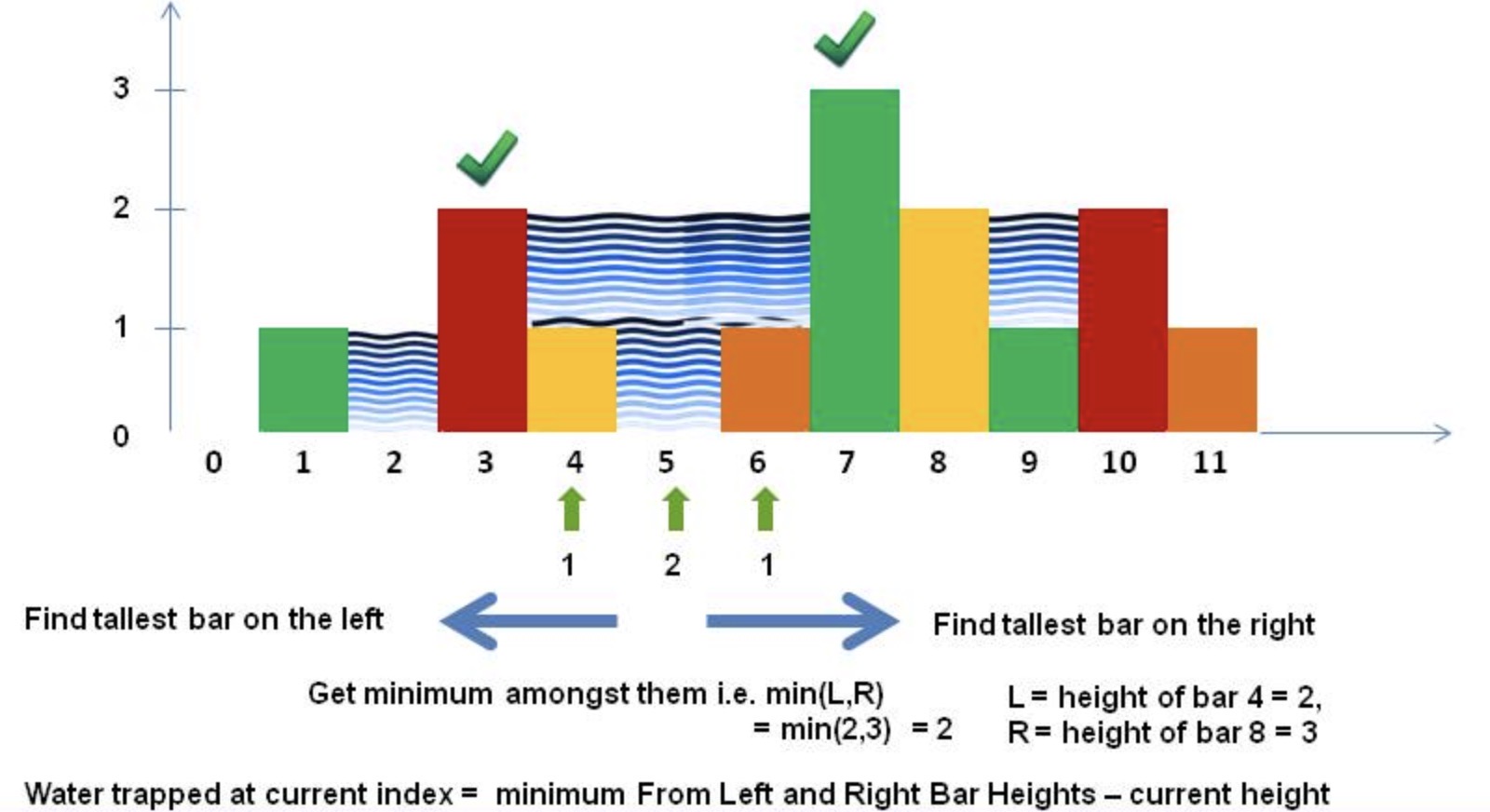
Given n non-negative integers representing an elevation map where the width of each bar is 1 unit, compute how much water it is able to trap after raining.Input: [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6
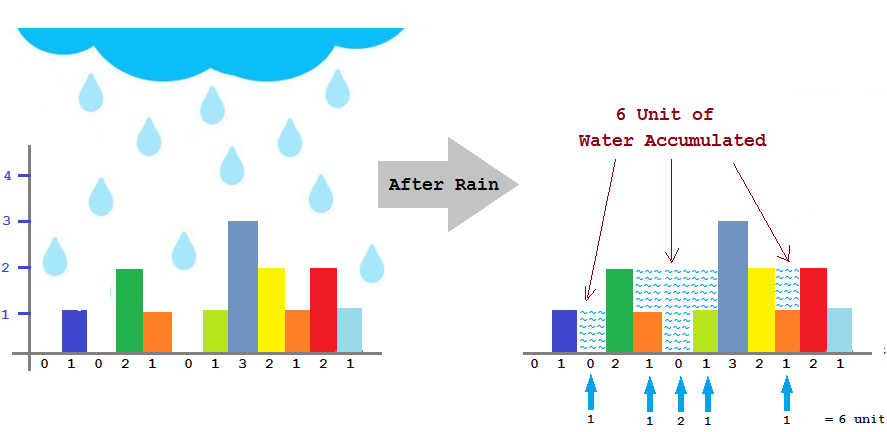
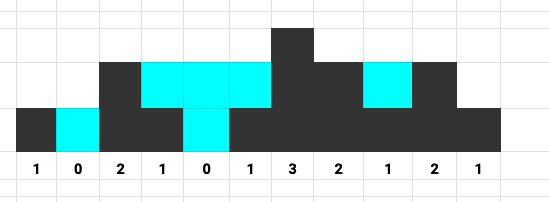
If you think through the problem for some time, you would soon be able to figure that
for each bar, to determine how much water will be accumulated on the bar we would need to know two things:
- What is the height of the highest bar on its left (including the current bar) ? Let's call it leftMax.
- What is the height of the highest bar on its right (including the current bar) ? Let's call it rightMax.
Let's suppose f(i) gives the value of the minimum of the two heights of the highest bar on the left and right of the i-th bar, say bars[i], then
f(i) = min(max(bars[0...i]), max(bars[i...n - 1)) = min(leftMax, rightMax)
It is important to observe that, if the height of the current bar is more that the minimum of the two heights of the left and right highest bars, then no water would be accumulated on that bar.
Below is a simple implementation which takes O(n) time and O(n) space, where n = total number of bars.
Since we need to calculate accumulated water on each bar, O(n) time is the best we can do. If you think more on how to optimize the solution for this problem, you would see that the optimization of the solution for this problem boils down to how efficiently we can compute the minimum of the heights of the left and right highest bar. While discussing the optimization we will see that, this optimization would primarily involve space optimization.
Let's take a look at the simple solution below which we would go on optimizing thoughout this chapter.
Java Code:
Login to Access Content
Python Code:
Login to Access Content
So, from the above discussion we have seen that the hurdle to solve the problem is to find the right maximum and left maximum. We have already seen the function f(i) = min(max(bars[0...i]), max(bars[i...n - 1)).
Let's see how the leftMax and rightMax would look like for bar[i], for i = 0 to (n - 1).
leftMax[0] = input[0]
rightMax[n - 1] = input[n - 1]
rightMax[n - 1] = input[n - 1]

input[] = [0,1,0,2,1,0,1,3,2,1,2,1]
leftMax = [0,1,1,1,2,2,2,3,3,3,3,3]
rightMax= [3,3,3,3,3,3,3,3,2,2,2,1]
leftMax curve would look like:
4 | _________________
3 | ___________/
2 | __________/
1 |__/________________________________________
0 1 2 3 4 5 6 7 8 9 10 11
rightMax curve would look like:
4 |_________________________
3 | \________________
2 | \_
1 |____________________________________________
0 1 2 3 4 5 6 7 8 9 10 11
If we plot both leftMax and rightMax in the same graph we get below curve for leftMax would look like:
leftMax and rightMax combined curve:
4 |____________________________________________
3 | ___________/ \____________
2 | ___________/ \_
1 |_/__________________________________________
0 1 2 3 4 5 6 7 8 9 10 11
What are important here to notice here are:
- leftMax is non-decreasing, from index 0 to n-1. It either remains constant or increases in value.
- rightMax is non-increasing, from index 0 to n-1. It either remains constant or decreases in value.
minOfLeftMaxRightMax[] = [0,1,1,1,2,2,2,3,2,2,2,1]
Graph for the Lower Envelope would look like:
min of leftMax and rightMax:
4 | ___
3 | ___________/ \____________
2 | ___________/ \_
1 |_/__________________________________________
0 1 2 3 4 5 6 7 8 9 10 11
If you have already noticed, The above curve is the LOWER ENVELOPE of leftMax and RightMax combined curve. We get this curve
by taking the minimum of the leftMax curve and rightMax curve for all index i.
This problem is all about finding the LOWER ENVELOPE of leftMax curve and rightMax curve for all index i = 0 to n-1.
If we want to optimize the previous solution, we should think about how to avoid computing leftMax and rightMax for all index i = 0 to n-1, because computing them separately takes O(n) space, which we are trying to optimize. To achieve this, let's re-analyze the characteristics of the different curves we plotted above.
From above plotted curves, our observations are:
- We have two MONOTONIC curve: leftMax and rightMax.
- leftMax curve is monotonically non-decreasing from left to right (i.e, from index 0 to n-1).
- rightMax curve is monotonically non-increasing from left to right (i.e, from index 0 to n-1). Or, we can say, rightMax is non-decreasing from right to left from index n-1 to 0.
input[] = [0,1,1,1,2,2,2,3,2,1,2,1]
We will have two pointers i and j and iterate over input array. Below is how we can create the lower envelope for all the indices 0 to n-1:
-
i = 0
j = 11
input[i] = 0
input[j] = 1
leftMax is 0 at index = i = 0.
leftMax is monotonically non-decreasing from left to right on index (0 to n-1). Which means, leftMax will either stay at 0 or will go up for higher index. So at index = j = 11 leftMax will be at least 0.
rightMax at index = j = 11 is 1. rightMax is non-decreasing from right to left (from index = n-1 to 0). This means, rightMax at index = i = 0 is at least 1.
So, minOfLeftMaxRightMax[0] = min(leftMax, rightMax) = min(0, at least 1) = 0
But, we cannot say the same thing about minOfLeftMaxRightMax[11]. At index = j = 11, we have rightMax = 1. We do not know what the true leftMax for index 11 will be as of now. All we can say we leftMax will be at least 0.
If leftMax[11] turns out to be > 1 then minOfLeftMaxRightMax[11] = leftMax[11], but if leftMax stays at 0 or grows higher only to 1, then minOfLeftMaxRightMax[11] = leftMax.
-
Since we got the true minOfLeftMaxRightMax value for minOfLeftMaxRightMax[0] we increment i by 1
to make i = 1.
j stays at index 11. - Repeat above step till we have LOWER ENVELOPE for all indices.
The below code will make the whole algorithm very clear.
Java Solution:
Login to Access Content
Python Code:
Login to Access Content
Another similar implementation :
Java Code:
Login to Access Content
Python Code:
Login to Access Content
Yet Another Approach:
Another O(n) time and O(1) space solution would be to find the index of the highest bar (say, Hmax) and then processing the bars on the left and right of it.- For computing for the bars on left of the highest bar Hmax, we would need to compute only the height of the highest bar on the left of the current bar.
- For computing for the bars on right of the highest bar Hmax, we would need to compute only the height of the highest bar on the right of the current bar.
This approach does not use Lower Envelope concept.
The code for this approach is given below:
Java Code:
Login to Access Content
Python Code:
Login to Access Content
